Определите наименьшее натуральное число, кратное 2, которое при делении на 11 с остатком дает неполное частное, равное 7.
Централизованное тестирование по математике, 2016
На рисунке изображен треугольник ABC, в котором ∠ACB = 35°, ∠AMN = 107°. Используя данные рисунка, найдите градусную меру угла BAC.
Используя рисунок, определите верное утверждение и укажите его номер.


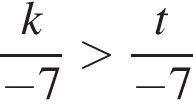
Значение выражения 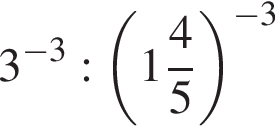 равно:
равно:
Укажите формулу для нахождения n-го члена арифметической прогрессии (an), если a1 = 4, a2 = 7.
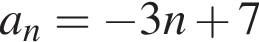
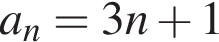
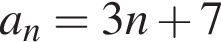
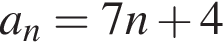
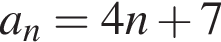
Величины a и b являются прямо пропорциональными. Используя данные таблицы, найдите неизвестное значение величины a.
| a | 1,3 | |
| b | 112 | 9,1 |
Найдите площадь фигуры, изображенной на рисунке.
Найдите сумму всех целых значений функции y = f(x), заданной графиком на промежутке (-5; 5) (см.рис.).
Найдите значение выражения НОК(8, 12, 48)+НОД(30,42).
Прямая a пересекает плоскость α в точке A и образует с плоскостью угол 60°. Точка B лежит на прямой a, причем AB = ![]() Найдите расстояние от точки B до плоскости α.
Найдите расстояние от точки B до плоскости α.
На круговой диаграмме показано распределение посевных площадей под зерновые культуры в агрохозяйстве. Сколько гектаров отведено под пшеницу, если гречихой засеяно на 550 га меньше, чем рожью?
Длины всех сторон треугольника являются целыми числами. Если длина одной стороны равна 1, а другой — 11, то периметр треугольника равен:
Сократите дробь 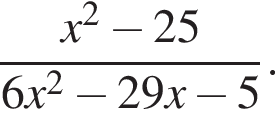
Из пунктов A и B, расстояние между которыми 120 км, одновременно навстречу друг другу выехали два автомобиля с постоянными и неравными скоростями: из пункта A — со скоростью a км/ч, из пункта B — со скоростью b км/ч. Через некоторое время автомобили встретились. Составьте выражение, определяющее расстояние (в километрах) от пункта B до места встречи автомобилей.
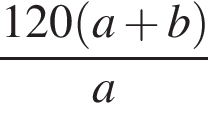
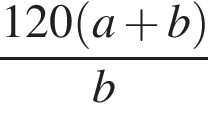
Точки A, B, C лежат на большой окружности сферы так, что треугольник ABC — равносторонний. Если AB = ![]() то площадь сферы равна:
то площадь сферы равна:
Упростите выражение 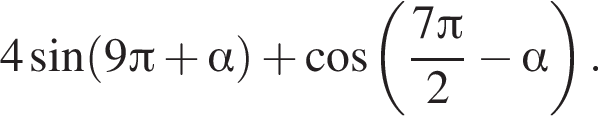


График функции, заданной формулой y = kx + b, симметричен относительно начала координат и проходит через точку A (3; 12). Значение выражения k + b равно:
Сумма всех натуральных решений неравенства 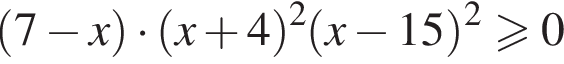 равна:
равна:
Для покраски стен общей площадью 175 м2 планируется закупка краски. Объем и стоимость банок с краской приведены в таблице.
| Объем банки (в литрах) | Стоимость банки с краской (в рублях) |
|---|---|
| 2,5 | 85 000 |
| 10 | 290 000 |
Какую минимальную сумму (в рублях) потратят на покупку необходимого количества краски, если ее расход составляет 0,2 л/м2?
Найдите сумму корней (корень, если он единственный) уравнения 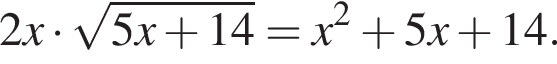
В равнобедренную трапецию, площадь которой равна ![]() вписана окружность. Сумма двух углов трапеции равна 60°. Найдите периметр трапеции.
вписана окружность. Сумма двух углов трапеции равна 60°. Найдите периметр трапеции.
Пусть (x; y) — решение системы уравнений 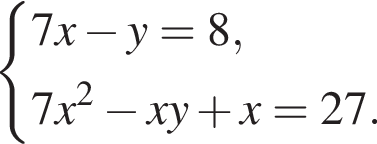
Найдите значение 7y − x.
Найдите значение выражения 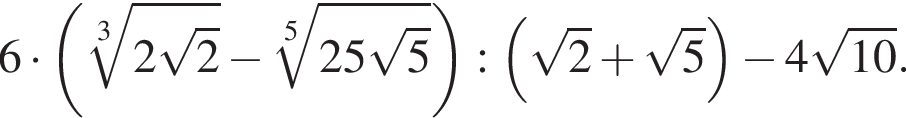
Найдите сумму корней уравнения 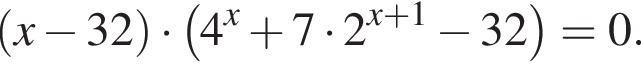
Найдите площадь боковой поверхности правильной треугольной пирамиды, если длина биссектрисы ее основания равна ![]() и плоский угол при вершине
и плоский угол при вершине 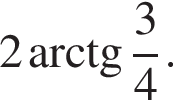
Найдите сумму наименьшего и наибольшего целых решений неравенства 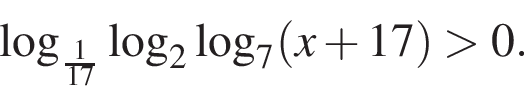
Найдите (в градусах) сумму корней уравнения  на промежутке (100°; 210°).
на промежутке (100°; 210°).
Найдите произведение наименьшего и наибольшего целых решений неравенства 
Точка A движется по периметру треугольника KMP. Точки K1, M1, P1 лежат на медианах треугольника KMP и делят их в отношении 11 : 2, считая от вершин. По периметру треугольника K1M1P1 движется точка B со скоростью, в семь раз большей, чем скорость точки A. Сколько раз точка B обойдет по периметру треугольник K1M1P1 за то время, за которое точка A два раза обойдет по периметру треугольник KMP?
Объем прямоугольного параллелепипеда ABCDA1B1C1D1 равен 864. Точка P лежит на боковом ребре CC1 так, что CP : PC1 = 2 : 1. Через точку P, вершину D и середину бокового ребра AA1 проведена секущая плоскость, которая делит прямоугольный параллелепипед на две части. Найдите объём большей из частей.

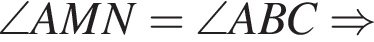
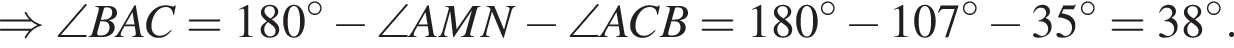
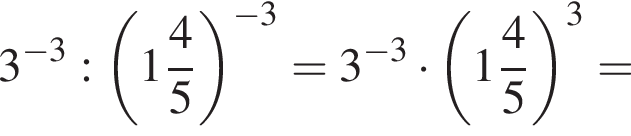
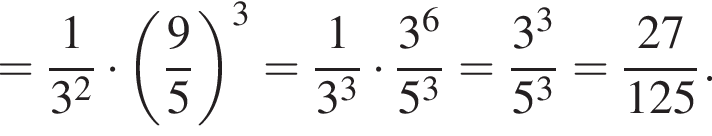
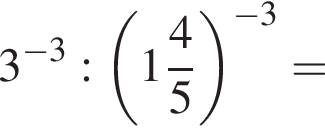
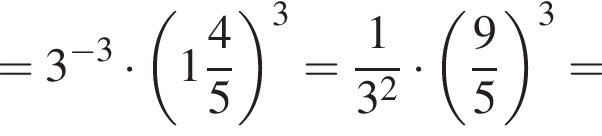
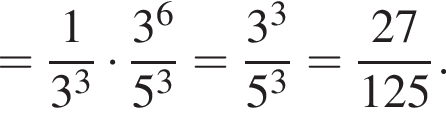
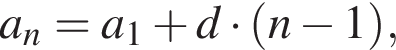 где d — разность арифметической прогрессии. Разность арифметической прогрессии равна
где d — разность арифметической прогрессии. Разность арифметической прогрессии равна  Поэтому
Поэтому 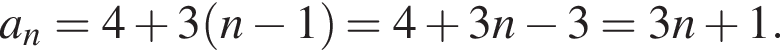
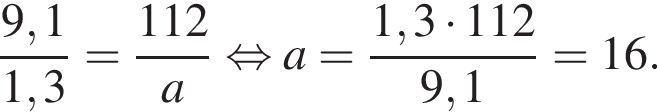
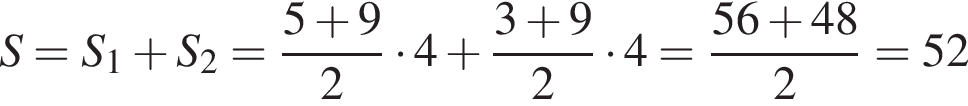
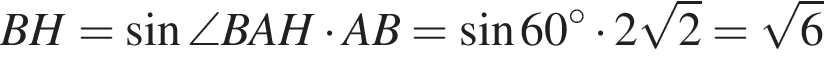
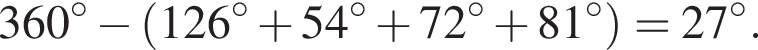 Известно, что длины дуг пропорциональны посевным площадям. Пусть x — площадь, засеянная гречихой. Тогда
Известно, что длины дуг пропорциональны посевным площадям. Пусть x — площадь, засеянная гречихой. Тогда 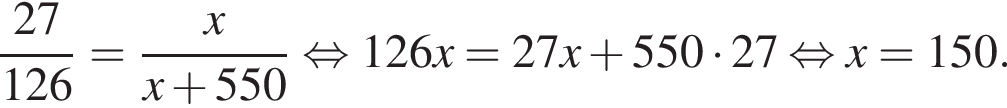
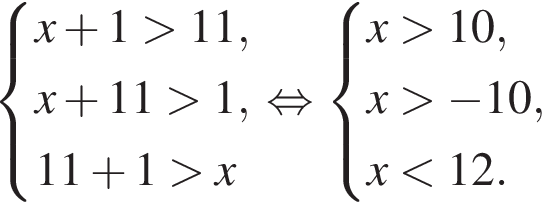
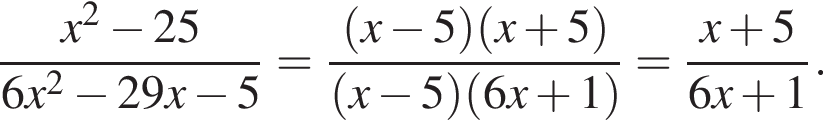
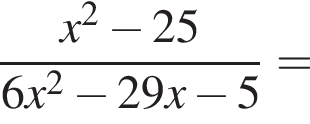
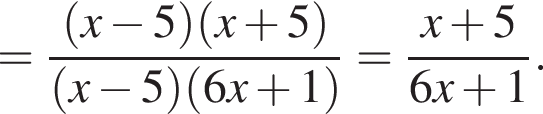
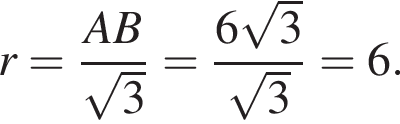 Площадь сферы равна
Площадь сферы равна 

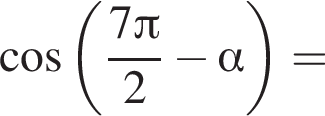
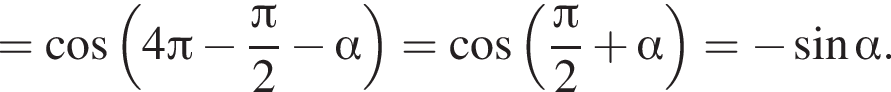
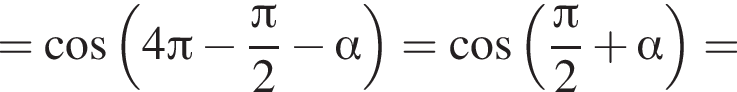
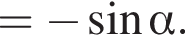
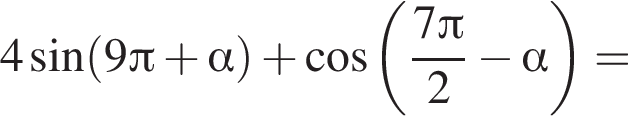

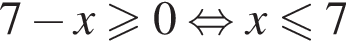 и
и  следовательно, натуральные решения неравенства: 1, 2, 3, 4, 5, 6, 7, 15. Их сумма равна 43.
следовательно, натуральные решения неравенства: 1, 2, 3, 4, 5, 6, 7, 15. Их сумма равна 43.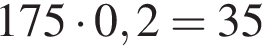 л краски. Можно купить 3 банки по 10 литров и 2 банки по 2,5 литра, тогда минимальная сумма составит:
л краски. Можно купить 3 банки по 10 литров и 2 банки по 2,5 литра, тогда минимальная сумма составит: 
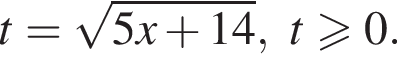 Тогда:
Тогда: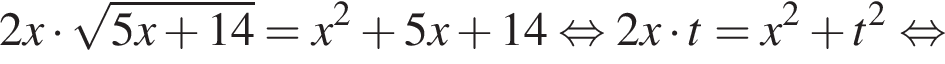

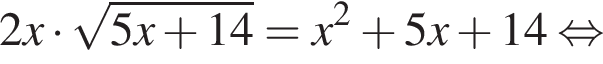


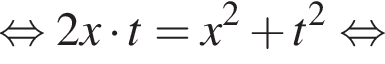
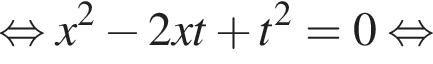
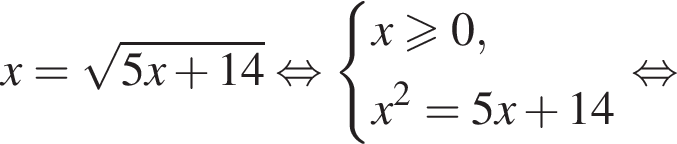
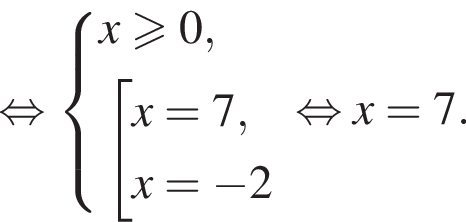
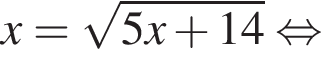
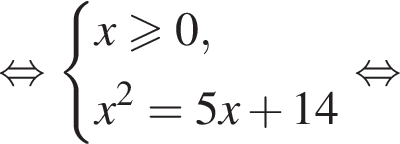
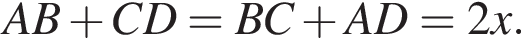 Сумма углов в равнобедренной трапеции, прилежащих к одной стороне равна 180°, откуда следует, что сумма углов, данная в условии — есть сумма углов при основании AD, которые равны.
Сумма углов в равнобедренной трапеции, прилежащих к одной стороне равна 180°, откуда следует, что сумма углов, данная в условии — есть сумма углов при основании AD, которые равны. 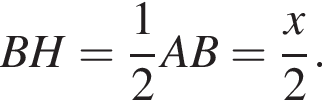 Поэтому из площади трапеции найдем x:
Поэтому из площади трапеции найдем x: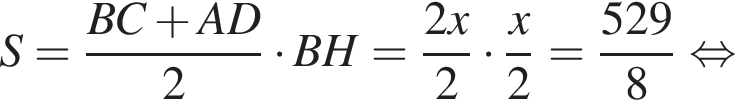
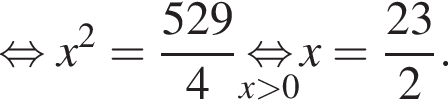
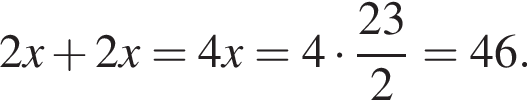
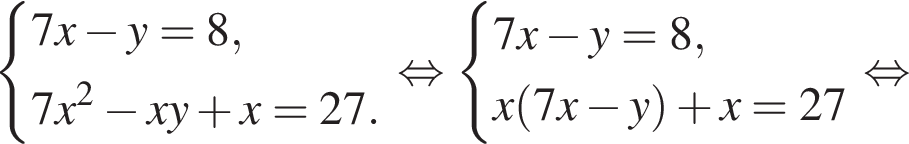
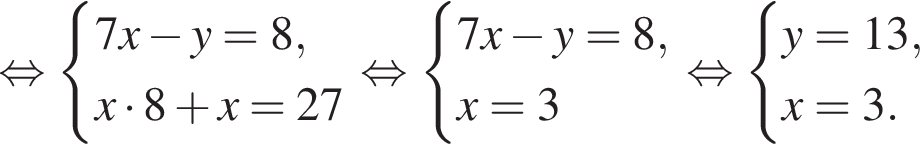
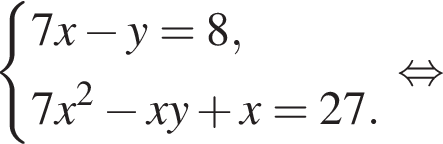
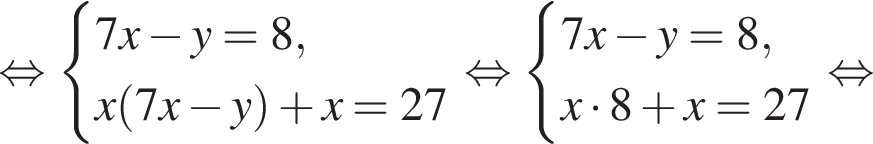
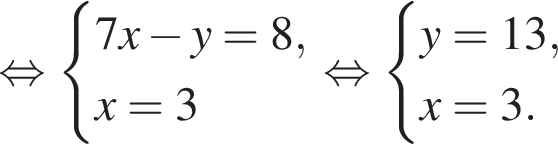
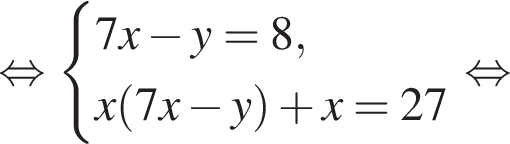
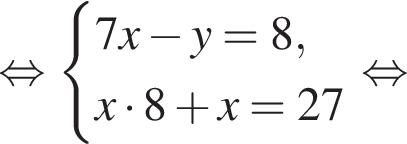
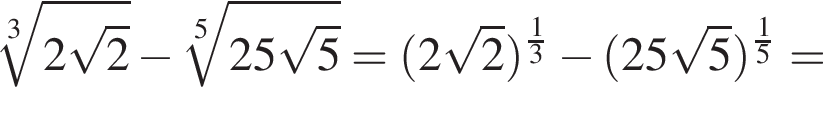
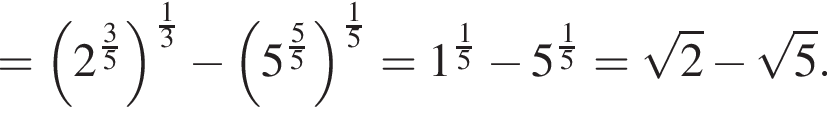
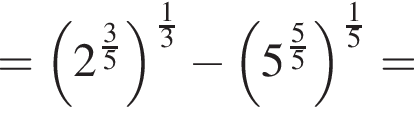
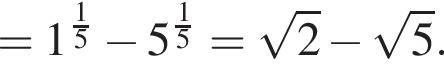
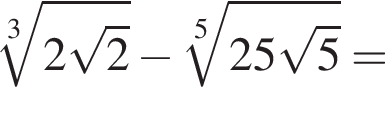
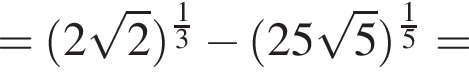
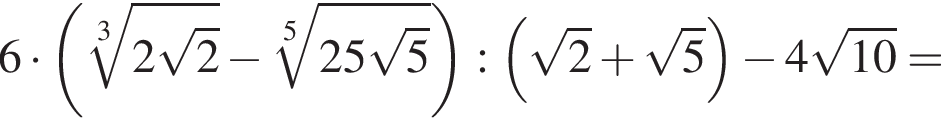
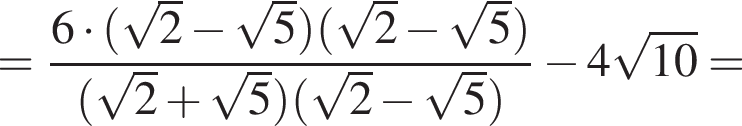
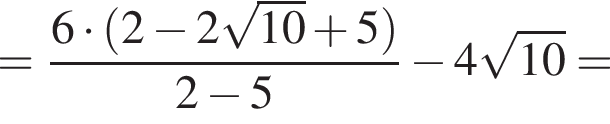

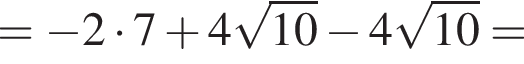
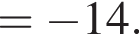
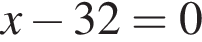 следует, что первый корень
следует, что первый корень 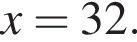 Рассмотрим
Рассмотрим 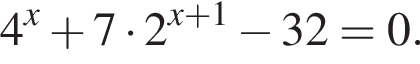 Сделаем замену
Сделаем замену 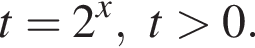 Тогда:
Тогда: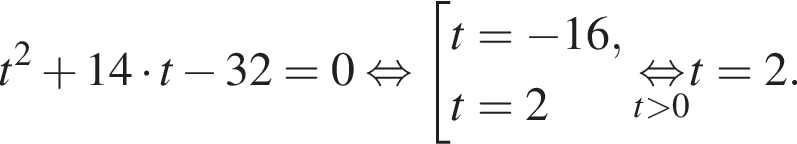
 Отсюда следует, что сумма корней уравнения равна 33.
Отсюда следует, что сумма корней уравнения равна 33.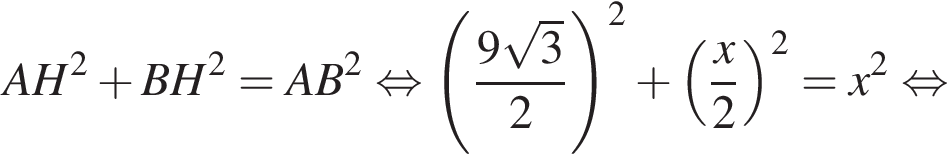
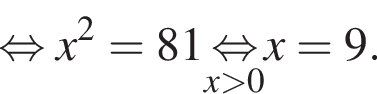
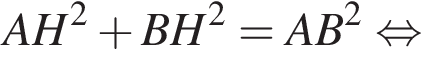
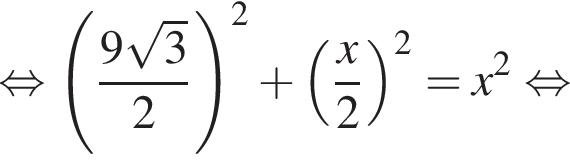
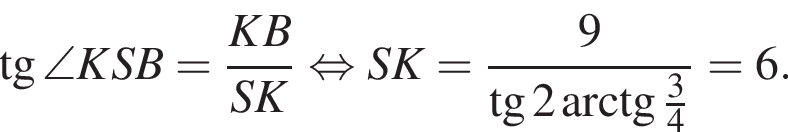 Площадь боковой поверхности равна
Площадь боковой поверхности равна 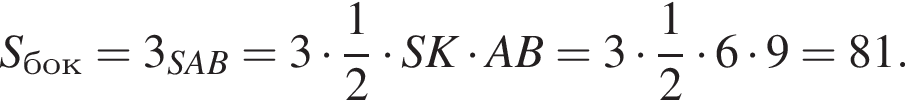
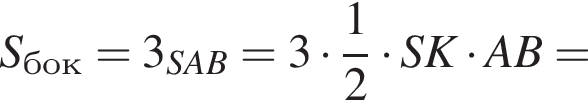
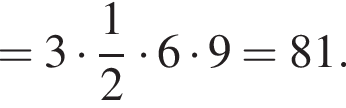
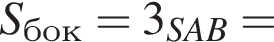
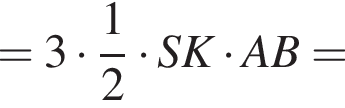

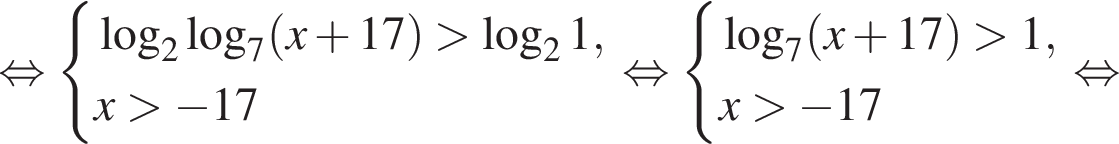
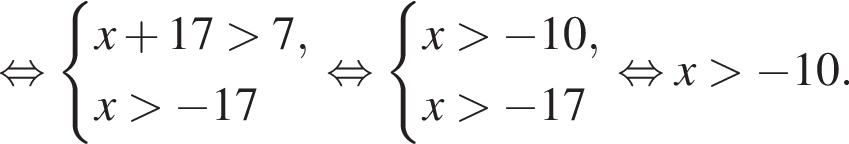
 тогда:
тогда: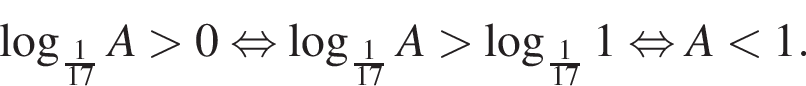
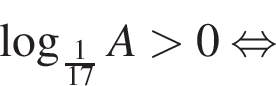
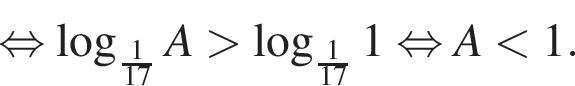

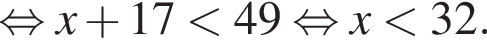

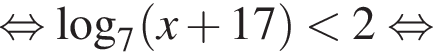
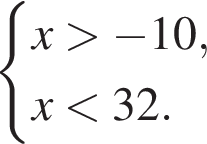 Поэтому наибольшее целое значение — 31, наименьшее целое значение −9, их сумма равна 22.
Поэтому наибольшее целое значение — 31, наименьшее целое значение −9, их сумма равна 22.
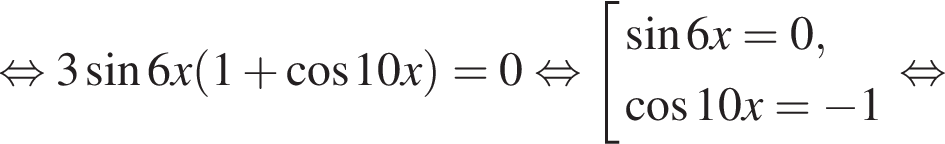
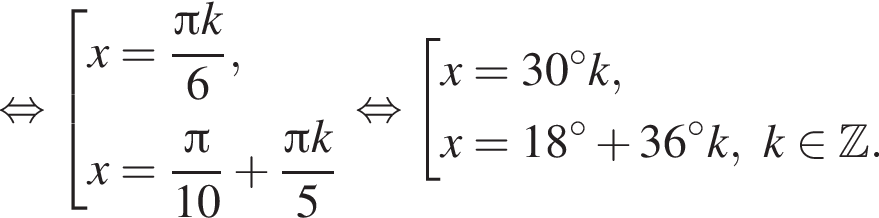
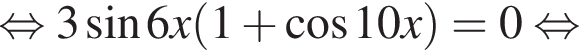
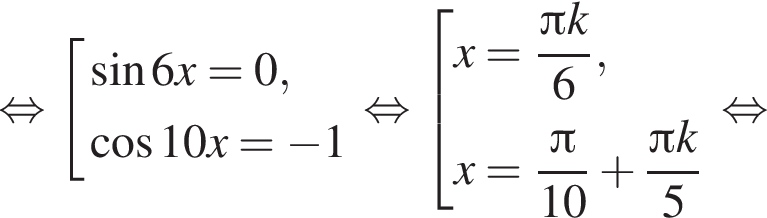
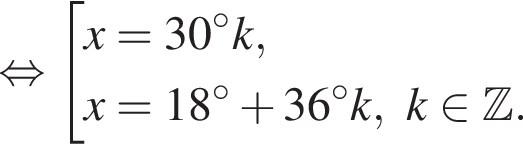
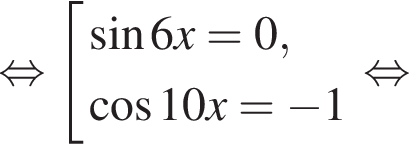
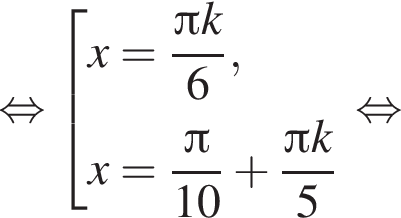
 имеем:
имеем: 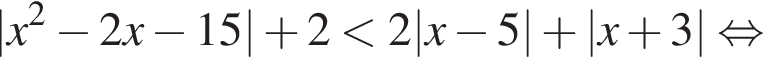
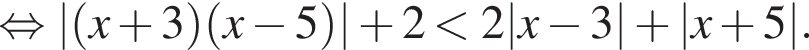
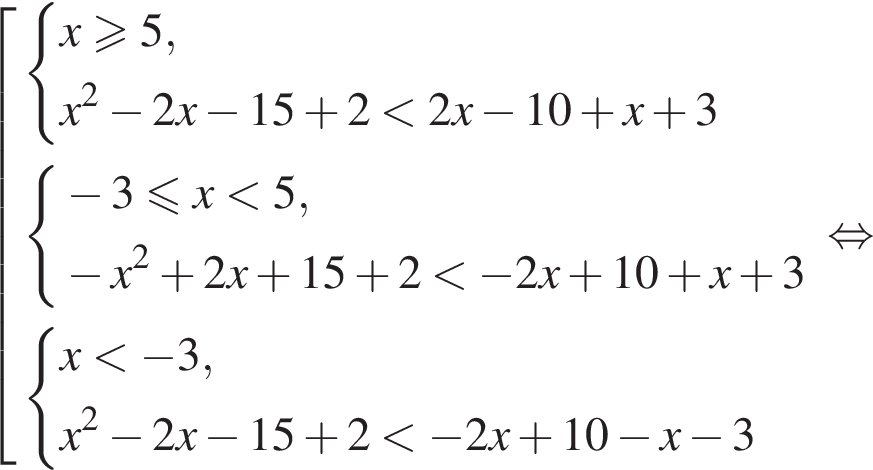
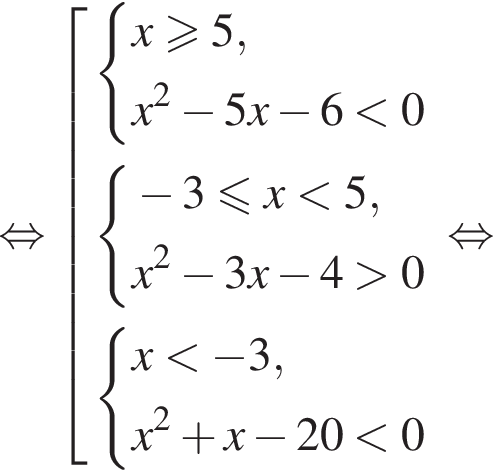
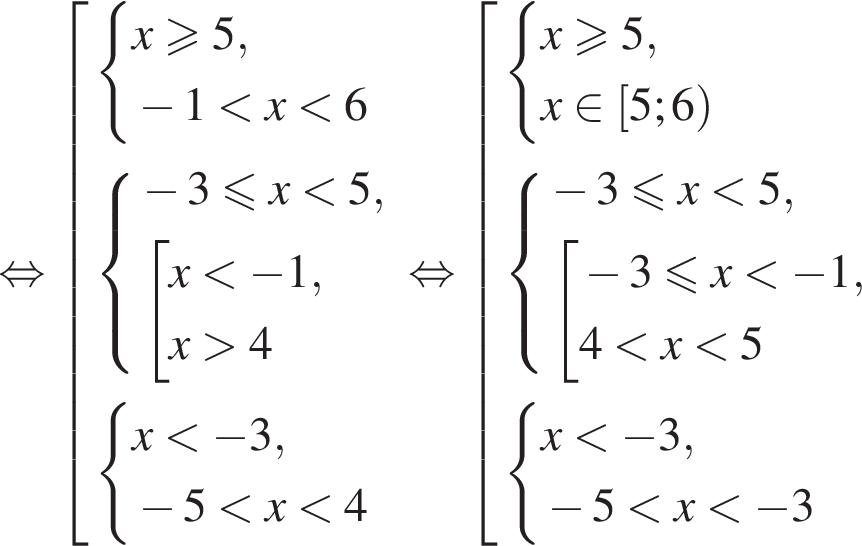
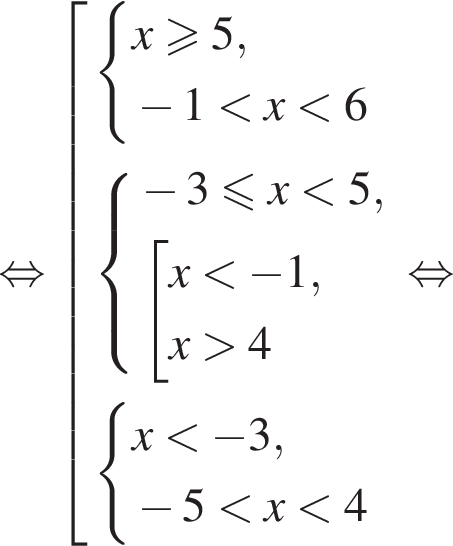
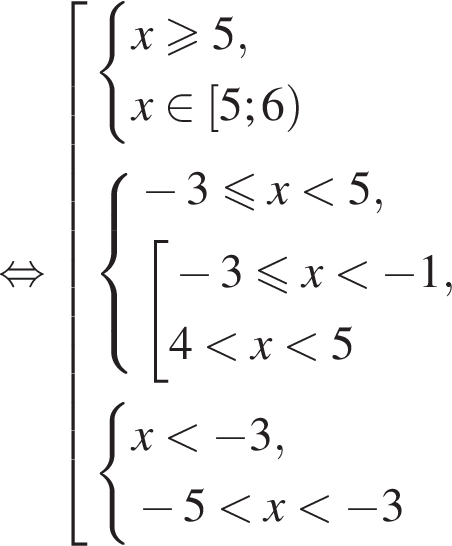
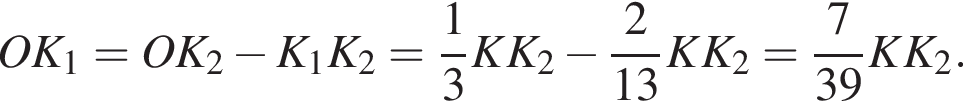
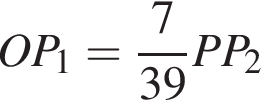 и
и 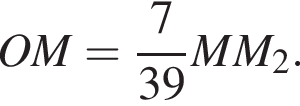
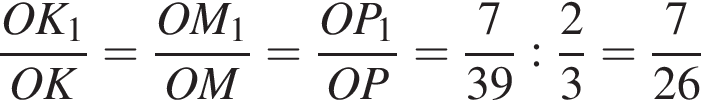 и треугольники M1K1P1 и MKP подобны, получаем
и треугольники M1K1P1 и MKP подобны, получаем 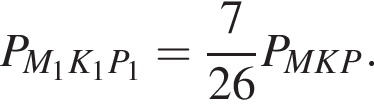 Тогда
Тогда 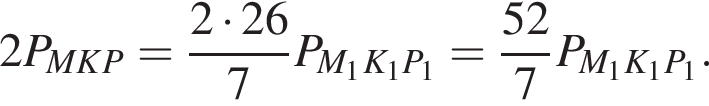 Тогда точка B обойдет периметр 52 раза.
Тогда точка B обойдет периметр 52 раза.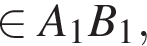 проведем KP||OM, K
проведем KP||OM, K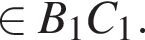 Таким образом, MNKPD — искомое сечение.
Таким образом, MNKPD — искомое сечение.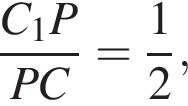 тогда
тогда 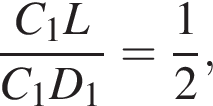 тогда
тогда 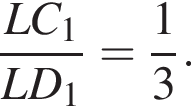
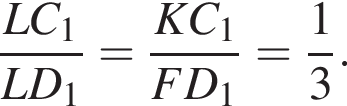 Аналогично находим отношение
Аналогично находим отношение 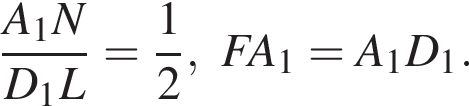
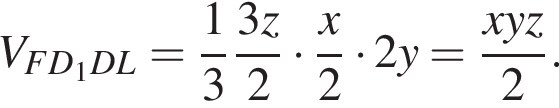
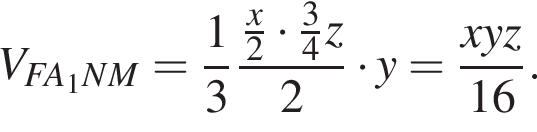
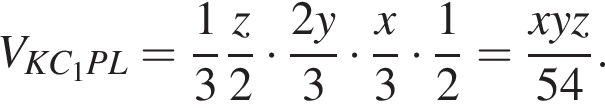
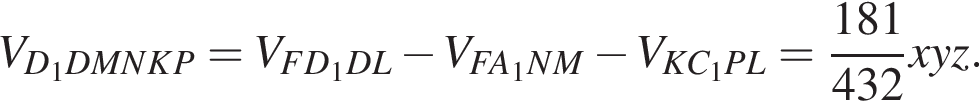
 следовательно, это не искомый объём. Тогда объём искомой части равен 502.
следовательно, это не искомый объём. Тогда объём искомой части равен 502.